Lean Six Sigma Forum
1 Sigma Defect Rate
Hello. The text (page 9) states that a process operating at one sigma has a defect rate of approximately 70%. However, the area under the normal curve at +/- 1 sigma covers 68% of the data. Wouldn't that mean that a process operating at 1 sigma has 32% defects (instead of 70%)? I am confused. Thanks for any feedback
Welcome to the Jungle!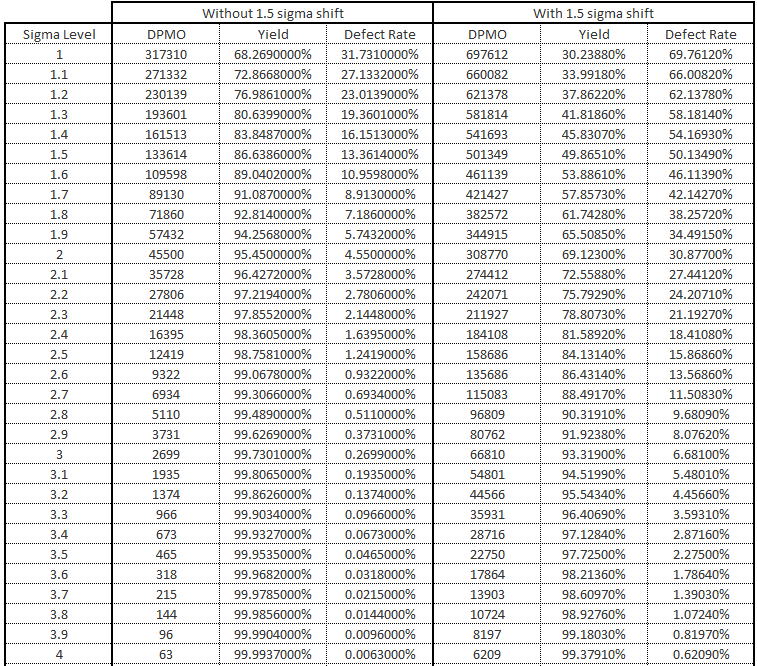
OHH, Stephen! - good question! This is going to spin into a hotly debated topic in the Six Sigma world that most people struggle with, and honestly, I'm not exempt myself. It would be much easier to operate in that black-and-white world where things are clear and simple, and our target doesn't move around. But that's not the world we live in, so here goes!
Your observation that ~68% of the data lies within +/- 1 sigma is very good and logical.
Now just for a moment, picture that distribution in your mind. It's just sitting there static and not "moving." This being the case, at that moment in time, yes, the defect rate would be around 32%.
But, and this is a big "But", in the Six Sigma world, we account for performance drift with what is called the 1.5 sigma shift. This is because, in real life, that distribution drifts around over the long term while the spec limits do not. Hence, over the long haul, the defect rate is ~70% under these circumstances.
The DPMO Sigma Level table included here should help explain this a bit. You can see with a 1.5 sigma shift, the defect rate for a 1 sigma process is about 70%, while "without" the shift (like the question you posed) it's more like the 32% as you expected.
Clear as mud 🙂 ??